新チョコレートゲーム 〜New Chocolate Games〜
関西学院高等部数理科学部が研究している数式を元にして作成したゲームです。
拙作「Bitter Chocolate Games 1」「Bitter Chocolate Games 2」「Bitter Chocolate Games 3」を
ベースとし、操作性の向上、最適化、および3つのゲームをまとめたゲームとなっています。
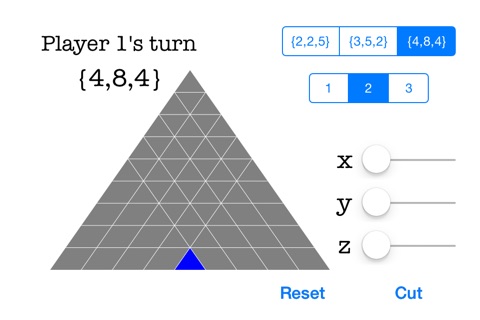
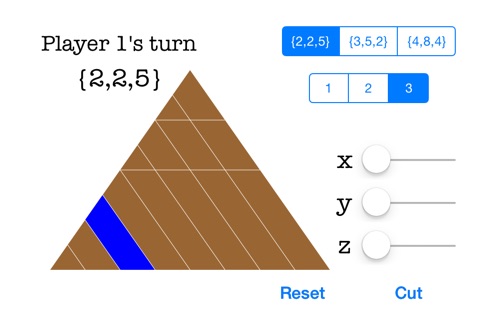
茶色(灰色)の部分は甘くて美味しいチョコレート、青い(赤い)チョコレートの部分は苦くて食べられないチョコレートで、甘い部分を全て食べ尽くし、苦くて食べられない部分だけを残された方が負けというシンプルなゲームです。
操作方法は以下の通りです。
(Player1とPlayer2の対戦形式となっています。)
(1) 右側のx,y,zのスライダを動かし、切りたいところにラインを合わせます。
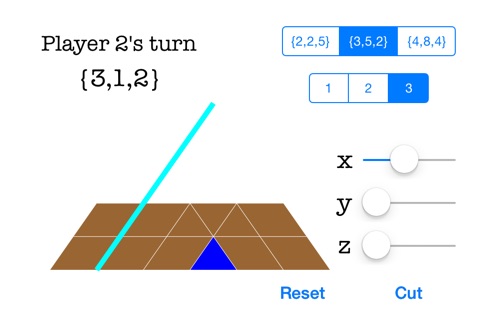
(2) 左下のcutをタップします(そこでチョコレートが切れます)。
(3) Player交代します(もちろん1人でも遊べます)。
この操作を繰り返します。
青い(赤い)チョコレートの部分(Bitter Chocolate Piece)だけを最後に残したPlayerが勝ちです。
右下のResetをタップすると一番最初の状態に戻ります。
さらに、左上のセグメントボタンでチョコレートの形状が変化します。
{x,y,z}は、チョコレートの座標を表しています。
数学的に証明されているこの新しいゲームで楽しんでいただければ幸いです。
応用として、このゲームには以下のような攻略のコツがあります。
・セグメント1のチョコレートの場合
{x,y,z}という形で、x,y,zの排他的論理和が0のときから始めると、相手が賢くプレーすれば負けます。
x,y,zの排他的論理和が0でないときから始めると、排他的論理和が0になるようにプレーすれば勝てます。
・セグメント2および3のチョコレートの場合
{x+1,y,z+1}という形で、x,y,zの排他的論理和が0のときから始めると、相手が賢くプレーすれば負けます。
x,y,zの排他的論理和が0でないときから始めると、排他的論理和が0になるようにプレーすれば勝てます。
References:
R. Miyadera, S. Nakamura and R. Hanafusa, New Chocolate Games -Variants of the Game of Nim-,
Proceeding of Annual International Conference on Computational Mathematics,
Computational Geometry Statistics,pp.122-pp.128, 2012.
Programming and App Making:Masanori Fukui(EM Software).
Icon,Layout and Color Design:Ryo Hanafusa(Kwansei Gakuin University).
App Test:Ryo Hanafusa and Masami Tsukamoto and Jo Hagikura(Kwansei Gakuin Senior High School).
Special Thanks to Ryohei Miyadera(Kwansei Gakuin High School) and Kwansei Gakuin High School Mathematical Sciences Club.